In this series I am reviewing some of my lecture notes of the first graduate course in probability.
Uniform Integrability - The definition
The sequence, \( X_n \), is called uniformly integrable if:
\[ \lim_{A \to \infty} \sup_n \mathbb{E} [|{X_n}| \mathbb{1}_{|{X_n}|>A}] = 0\]
What does this formula tells us?
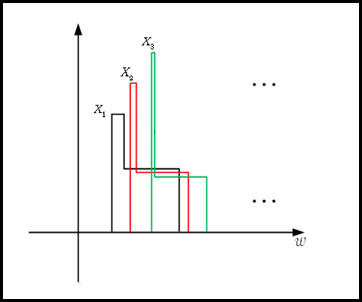
Lets start with the \( |{X_n}| \mathbb{1}_{|{X_n}|>A}\) term. This term actually means that we “reset” \( |{X_n}| \) to zero where ever it is below \(A\) and leave it untouched where ever it is above \(A\). Look at the figure below:
Next, look at \(\mathbb{E} [|{X_n}| \mathbb{1}_{|{X_n}|>A}] \). This is the aria under the graph of \( |{X_n}| \mathbb{1}_{|{X_n}|>A}\) (the aria relative to the probability measure in question \(dP(\omega)\) here I suppose that the probability space is, say, \(\omega \in [0,M]\) with uniform probability measure so that \(dP(\omega)= \frac{1}{M}\)). The supremum \(\sup_n\) picks the \(n\) for which the corresponding graph gives the biggest area for fixed \(A\).
Finally, by taking the limit \(\lim_{A \to \infty} \sup_n \mathbb{E} [|{X_n}| \mathbb{1}_{|{X_n}|>A}]\), we examine what happens with that area when \(A\) grows bigger and bigger.
Here are two sequences of random variables, first is not uniformly integrable and the second is:
This is not uniformly integrable sequence, since no matter how big \(A\) grows, there is always some \(n\) for which \(\mathbb{E} [|{X_n}| \mathbb{1}_{|{X_n}|>A}]\) equals 1, for big enough \(n\), \(|{X_n}| \mathbb{1}_{|{X_n}|>A} \) is just \( |{X_n}|\). So \( \sup_n \mathbb{E} [|{X_n}| \mathbb{1}_{|{X_n}|>A}] = \sup_n \mathbb{E} [|{X_n}|] = \sup_n 1 = 1\).
The sequence below is a uniformly integrable one:
By the way, do notice that both sequence converge to zero in probability ( \( \lim_{n \to \infty} P(X_n – 0) = 1) \) ).
Some Intuition:
So what we got here? The intuition is complicated, I haven't found any elegant way to describe it. The restrain imposed by uniform integrability is related to the behavior of the sequence in the limit of \(n\), and to the way the sequence goes to the infinity:
- It is easy to see that if the average aria below the graph of \(X_n\) is running away to infinity as \(n\) grow, then it is not uniformly integrable.
On the other hand -
- Any finite sequence is always uniformly integrable (since for any fixed \(n\) the \(P(X_n >A)\) inevitably decreases as \(A\) grows big)
- Any bounded sequence [bounded in a sense opposite to unbounded sequence. Unbounded that is as \(n\) grows bigger, the random variables, \(X_n\), can receive bigger and bigger values with some probability] is uniformly integrable. But the inverse is not true -
Here, I tried to draw unbounded sequence that is uniformly integrable since the average shrinks as \(n\) grows bigger.
Technorati Tags: probability,random process,Uniform integrable
WordPress Tags: probability,random process,Uniform integrable
Blogger Labels: probability,random process,Uniform integrable



4 comments:
very helpful!
For the both cases, how is it that they converges in probability to 0? If the first case has X_n getting larger and larger, and the second with X_n constant as 1, how does this work? Or are you defining the X_n to be 1/2,1/3, etc?
Hey Thanks. That was super helpful.
Post a Comment